8. Cross validation

The term instance hardness is used in literature to express the difficulty to correctly classify an instance. An instance for which the predicted probability of the true class is low, has large instance hardness. The way these hard-to-classify instances are distributed over train and test sets in cross validation, has significant effect on the test set performance metrics. The InstanceHardnessCV splitter distributes samples with large instance hardness equally over the folds, resulting in more robust cross validation.

We will discuss instance hardness in this document and explain how to use the InstanceHardnessCV splitter.

8.1. Instance hardness and average precision

Instance hardness is defined as 1 minus the probability of the most probable class:

\[H(x) = 1 - P(\hat{y}|x)\]

In this equation \(H(x)\) is the instance hardness for a sample with features \(x\) and \(P(\hat{y}|x)\) the probability of predicted label \(\hat{y}\) given the features. If the model predicts label 0 and gives a predict_proba output of [0.9, 0.1], the probability of the most probable class (0) is 0.9 and the instance hardness is 1-0.9=0.1.

Samples with large instance hardness have significant effect on the area under precision-recall curve, or average precision. Especially samples with label 0 with large instance hardness (so the model predicts label 1) reduce the average precision a lot as these points affect the precision-recall curve in the left where the area is largest; the precision is lowered in the range of low recall and high thresholds. When doing cross validation, e.g. in case of hyperparameter tuning or recursive feature elimination, random gathering of these points in some folds introduce variance in CV results that deteriorates robustness of the cross validation task. The InstanceHardnessCV splitter aims to distribute the samples with large instance hardness over the folds in order to reduce undesired variance. Note that one should use this splitter to make model selection tasks robust like hyperparameter tuning and feature selection but not for model performance estimation for which you also want to know the variance of performance to be expected in production.

8.2. Create imbalanced dataset with samples with large instance hardness

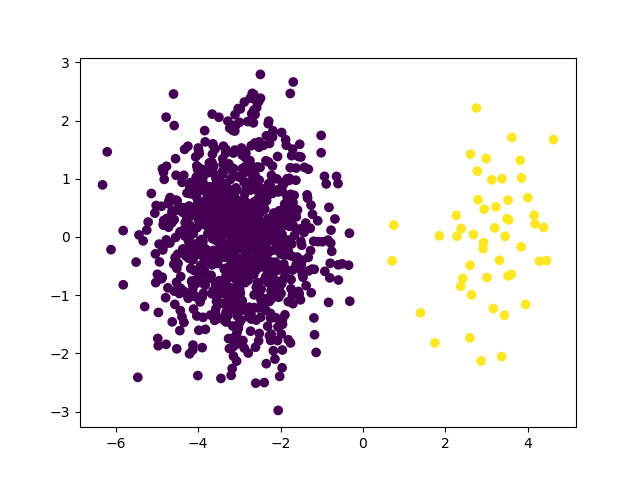
Let’s start by creating a dataset to work with. We create a dataset with 5% class imbalance using scikit-learn’s make_blobs function.

>>> import numpy as np
>>> from matplotlib import pyplot as plt
>>> from sklearn.datasets import make_blobs
>>> from imblearn.datasets import make_imbalance
>>> random_state = 10
>>> X, y = make_blobs(n_samples=[950, 50], centers=((-3, 0), (3, 0)),
...                   random_state=random_state)
>>> plt.scatter(X[:, 0], X[:, 1], c=y)
>>> plt.show()

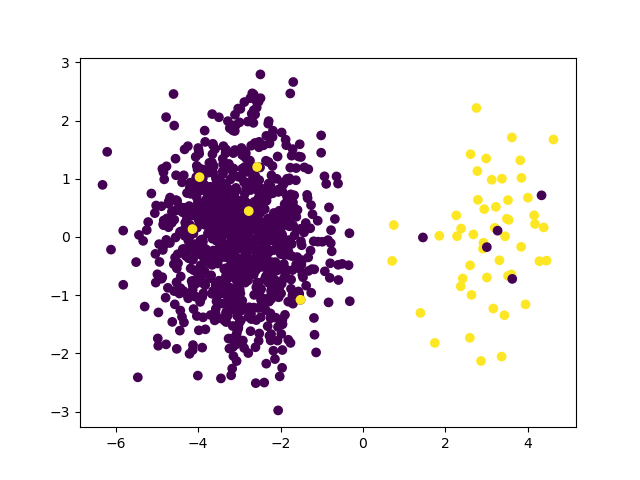
Now we add some samples with large instance hardness

>>> X_hard, y_hard = make_blobs(n_samples=10, centers=((3, 0), (-3, 0)),
...                             cluster_std=1,
...                             random_state=random_state)
>>> X = np.vstack((X, X_hard))
>>> y = np.hstack((y, y_hard))
>>> plt.scatter(X[:, 0], X[:, 1], c=y)
>>> plt.show()

8.3. Assess cross validation performance variance using InstanceHardnessCV splitter

Then we take a LogisticRegression and assess the cross validation performance using a StratifiedKFold cv splitter and the cross_validate function.

>>> from sklearn.ensemble import LogisticRegressionClassifier
>>> clf = LogisticRegressionClassifier(random_state=random_state)
>>> skf_cv = StratifiedKFold(n_splits=5, shuffle=True,
...                           random_state=random_state)
>>> skf_result = cross_validate(clf, X, y, cv=skf_cv, scoring="average_precision")

Now, we do the same using an InstanceHardnessCV splitter. We use provide our classifier to the splitter to calculate instance hardness and distribute samples with large instance hardness equally over the folds.

>>> ih_cv = InstanceHardnessCV(estimator=clf, n_splits=5,
...                               random_state=random_state)
>>> ih_result = cross_validate(clf, X, y, cv=ih_cv, scoring="average_precision")

When we plot the test scores for both cv splitters, we see that the variance using the InstanceHardnessCV splitter is lower than for the StratifiedKFold splitter.

>>> plt.boxplot([skf_result['test_score'], ih_result['test_score']],
...               tick_labels=["StratifiedKFold", "InstanceHardnessCV"],
...               vert=False)
>>> plt.xlabel('Average precision')
>>> plt.tight_layout()

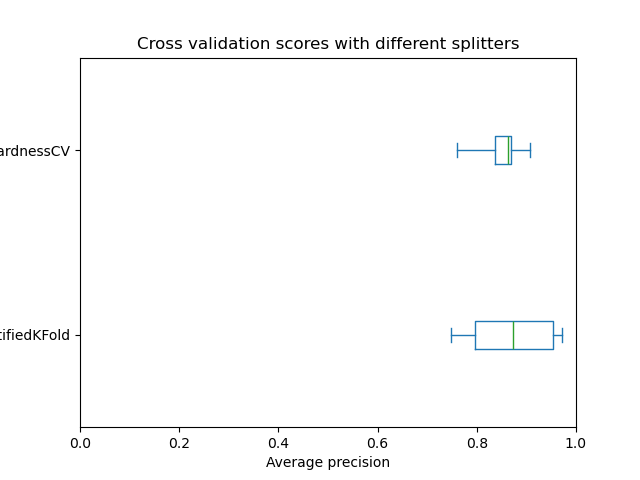
Be aware that the most important part of cross-validation splitters is to simulate the conditions that one will encounter in production. Therefore, if it is likely to get difficult samples in production, one should use a cross-validation splitter that emulates this situation. In our case, the StratifiedKFold splitter did not allow to distribute the difficult samples over the folds and thus it was likely a problem for our use case.